原文链接(文汇报):http://wenhui.whb.cn/zhuzhanapp/xue/20220620/472696.html
运用牛顿的万有引力理论能准确预测两个互相吸引的天体之运动规律——它们的轨道基本是椭圆形的。但如果有三个天体,比如太阳、地球和月球相互作用,其运行有何规律?科幻作家刘慈欣在其科幻小说《三体》中虚构了一个“三体世界”,向公众科普了牛顿1687年提出的这个著名的“三体问题”。小说中,“三体人”生活的行星在一个由三颗恒星组成的三体系统中运行,这三颗恒星的运动毫无规律,“三体人”的天空时常同时出现二个、三个太阳或者一个太阳也没有,导致“三体人”的星球不定期发生生命灭绝,“三体文明”不断毁灭与重生。
300余年来,“三体问题”得到国际学术界的广泛关注,成为历史上最著名的科学问题之一。近期,上海交通大学廖世俊教授和其博士生杨宇,以及暨南大学李晓明副教授在国际杂志《New Astronomy》发表论文,通过将“机器学习”与其发明的一种极高精度的数值算法相结合,提出了求解“三体问题”周期轨道的路线图,大大提高了计算效率,为获得“三体问题”海量、精确的周期轨道铺平了道路。
困扰科学家300余年的“三体问题”
自牛顿提出“三体问题”300余年(1687至1993年),科学家仅仅发现“三体问题”的三类周期轨道。
为什么“三体问题”周期轨道如此难找?
1890年法国科学家庞加莱发现,三体系统的运动轨道对初始条件非常敏感,任何微小扰动都会迅速增长,造成轨道很大的偏离;他还发现,三体系统各个星球运动的轨道通常不是周期性的,没有解析解。
这种轨迹对微小扰动的敏感性,1963年被美国科学家劳伦茨再次发现,并提出著名的“蝴蝶效应”:北美洲的一个飓风,很可能是几周前远在南美洲的一只蝴蝶扇了几下翅膀所引发的!这种敏感特性的发现标志着混沌动力学的诞生,它与量子力学、相对论被认为是20世纪最伟大的三大物理理论之一。
“三体问题”的混沌性质,也正是科幻小说《三体》中“三体文明” 不断毁灭的科学依据。
理论上讲,正是因为“三体问题”本质上的混沌性,导致采用传统的数值方法亦很难在一个较长时域内获得三体系统的准确轨道。
众所周知,任何数值计算都存在误差。但2006年劳伦茨发现,数值误差同样会导致混沌系统的轨迹迅速偏离:如果采用双精度数据编程,用计算机数值求解混沌动力系统,任何算法都不能获得收敛的混沌轨迹!
因此,即便在计算机性能达到每秒100亿亿次量级的2013年,塞尔维亚科学家舒瓦科夫和什诺维奇采用传统数值方法也仅发现“三体问题”11类周期轨道。其杰出的工作是“三体问题”的一个重大突破,但也从侧面反映出求解“三体问题”周期轨道之艰难。
中国科学家提出求解“三体问题”周期轨道的路线图
科学家们一直在探索“三体问题”的奥秘。2009年,上海交通大学廖世俊提出一个获得混沌动力系统收敛轨迹的策略——精准数值模拟(Clean Numerical Simulation),简称CNS。
CNS能将数值误差降到任意小,从而可获得混沌系统足够长时间内收敛的数值解,在理论上为准确获得“三体问题”的周期轨道铺平了道路。
基于CNS,2017年廖世俊团队成功获得等质量的“三体问题”695类周期轨道;2018年廖世俊团队与上海交通大学物理和天文学院景益鹏院士合作,应用CNS进一步成功获得两个质量相等的三体系统1349类全新的周期轨道。
任意不等质量的三体系统之周期轨道的获取更为困难。2021年廖世俊与暨南大学李晓明等合作,以一个已知的、具有相同质量的三体系统周期轨道为基础,成功应用CNS获得该三体系统任意不等质量的135445个周期轨道,将“三体问题”周期轨道数量增加了几个数量级,证实了CNS求解任意质量“三体问题”周期轨道(特别是长周期轨道)的有效性。值得指出的是,这135445个周期轨道很多是稳定的,其质量范围与2019年诺贝尔物理奖获得者麦耶(Michel Mayor)和奎洛兹(Didier Queloz)所发现的太阳系外第一个环绕类太阳恒星的行星相近,因此,这些周期轨道很有可能在宇宙中确实存在,今后有可能被观测到。
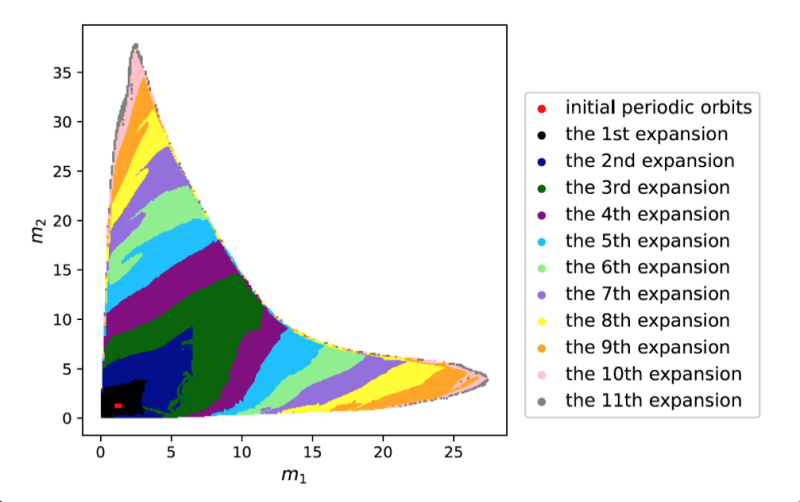
图1:利用机器学习寻找同一族三体系统不同星球质量的周期轨道。左下角红色区域为用传统方法获得的少数已知周期轨道。相同颜色表示同一次外插、机器学习可以找到的周期轨道之最大区域。m1和m2为两个星球质量(m3 = 1)。
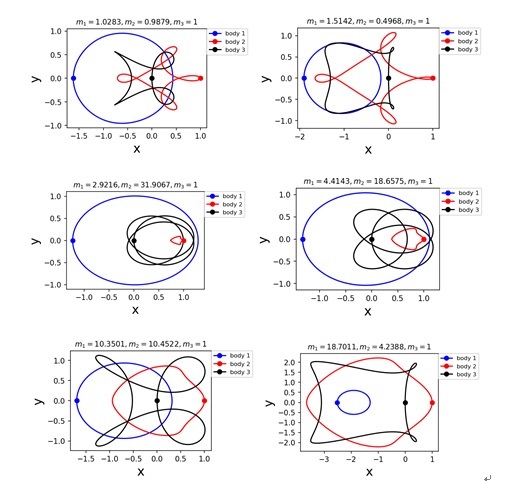
图2:机器学习预测的不同质量的“三体问题”周期解所模拟的周期轨道。蓝线:第一个星球;红线:第二个星球;黑线:第三个星球。
2022年,为了进一步大幅提高计算效率,廖世俊、李晓明、杨宇将CNS结合机器学习(一种从数据中分析获得规律,并利用该规律对未知数据进行预测的算法),提出了一个获得“三体问题”周期轨道的路线图。
从用传统方法获得的、很小质量范围内的周期轨道出发,基于机器学习和CNS一步步地获得更大质量范围内的精确周期轨道,直至找到该类周期轨道中所有不同质量的精确周期轨道,如图1所示。最后,对于(存在周期轨道的质量区域内)任意质量的“三体问题”,机器学习都能足够精确地预测其周期轨道之初始条件、周期,如图2所示。
该论文2022年在国际天文学杂志《New Astronomy》上发表(https://doi.org/10.1016/j.newast.2022.101850),其相关机器学习程序和周期轨道可在GitHub (https://github.com/sjtu-liao/three-body) 免费下载。
按上述策略采用CNS获得的“三体问题”之周期轨道可达到极高精度:即使以宇宙直径为特征长度,其初始位置的误差也远小于物理学上最小的距离单位 ——普朗克长度。根据广义相对论和量子力学,我们无法对位置做出比“普朗克长度”还要小、还要精确的测量;而且,比“普朗克长度”更短的长度是没有物理意义的。因此,进一步提高周期轨道的计算精度没有任何物理意义,所以采用CNS获得的“三体问题”之周期轨道就是物理意义上的精确轨道。
“三体问题”的解决,本质上依赖高性能计算机和数学方法。廖世俊等基于CNS和机器学习提出求解“三体问题”周期轨道之路线图,将计算效率提高了几个数量级,为获得“三体问题”海量的、精确的周期轨道铺平了道路。“三体问题”周期轨道的求解,证实了CNS求解复杂混沌问题的有效性和潜力。理论上,CNS可应用于N体问题周期轨道的求解以及湍流研究等,为星系演化、复杂湍流的精确数值模拟等提供了一个全新的研究工具。